直角三角形是一种特殊的三角形，其中包含一个90度的直角。它的面积可以通过以下公式计算：面积 = 底边长度 × 高 / 2。
其中，底边是直角边之一，高是另一直角边到底边的垂直距离。
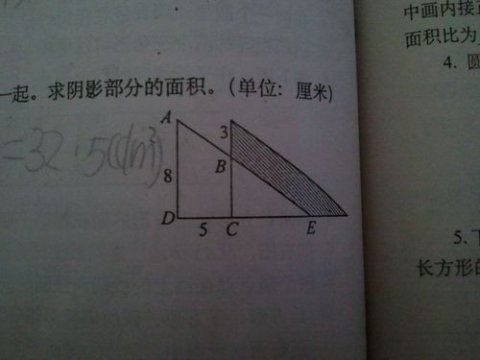
例如，如果一条直角边长为5厘米，另一条直角边长为3厘米，则面积为：5 × 3 / 2 = 7.5平方厘米。
这个公式的推导可以通过几何学的知识来解释。直角三角形可以被视为一个矩形的一半，其中直角边是矩形的一条边，高是矩形的高，并且三角形的另一条边是矩形的一半。直角三角形的面积等于矩形面积的一半。而矩形的面积是底边长度乘以高。
我们还可以使用勾股定理来计算直角三角形的面积。勾股定理指出，在一个直角三角形中，直角边的平方等于另外两条边的平方之和。
例如，在上述例子中，我们可以使用勾股定理来计算斜边的长度：32 + 52 = 34，因此斜边长为√34。然后，我们可以使用公式面积 = 1/2 × 底边长度 × 斜边长度来计算面积：1/2 × 5 × √34 ≈ 7.5平方厘米。
直角三角形的面积可以使用基本公式面积 = 底边长度 × 高 / 2来计算，也可以使用勾股定理和公式面积 = 1/2 × 底边长度 × 斜边长度来计算。
直角三角形的面积计算通常使用以下公式：$S=\frac{1}{2}ab$，其中$a$和$b$是直角三角形的两条直角边，$S$是直角三角形的面积。
具体而言，我们可以使用以下步骤计算直角三角形的面积：
步骤1：确定直角边和斜边
直角三角形的两条边中，其中一条是与直角相邻的边，我们称其为直角边；而另一条边则与直角不相邻，我们称其为斜边。
步骤2：确定直角边的长度
我们需要测量或知道直角边的长度。
步骤3：确定斜边的长度
我们需要测量或知道斜边的长度。
步骤4：使用勾股定理求另一条直角边的长度
勾股定理指出，在一个直角三角形中，直角边的平方和等于斜边的平方。
我们可以使用以下公式求出缺失的一条直角边的长度：$a^2+b^2=c^2$，其中$c$是斜边的长度。
步骤5：使用面积公式计算面积
通过已知的直角边和斜边的长度，和刚刚求出的另一条直角边的长度，我们可以使用面积公式计算出直角三角形的面积。具体而言，我们可以使用以下公式：$S=\frac{1}{2}ab$，其中$a$和$b$是直角三角形的两条直角边，$S$是直角三角形的面积。
总结起来，求解直角三角形面积的步骤包括确定直角边的长度、斜边的长度、使用勾股定理求另一条直角边的长度，最后使用面积公式计算出直角三角形的面积。
